En travaillant sur le contrôle et la réduction de la latence dans une application multi-media temps réel, j’ai découvert que le premier problème que j’avais était du aux variations de latence introduites par le réseau. La principale difficulté a été d’arriver a estimer le désordre produit par le réseau sur un flux RTP entrant sans pouvoir utiliser RTCP ou n’importe que autre canal de feed-back. Dans l’article suivant, nous allons nous intéresser a la méthode que j’ai utilisé pour estimer le désordre et déduire une taille optimale de buffers pour les conditions courantes.

Contexte

Partons d’une application qui transmet un flux audio et/ou vidéo temps reel à un receveur. Par temps réel, on entend que le contenu envoyé peut être interactif, ne peut pas être envoyé à l’avance au receveur (un appel audio ou vidéo par exemple). Il faut donc trouver un compromis entre l’interactivité (une latence faible) et un contenu diffusé de manière fluide (une latence plus élevée du à l’usage d’un tampon).

La source émet un flux à travers le réseau en direction du receveur. Souvent le contenu encodé (compressé) est découpé en de petites « access units » qui seront encapsulées dans des paquets RTP et envoyées par UDP. Pour simplifier nous considèrerons que la source se contente d’envoyer un flux video en utilisant RTP par dessus UDP en direction de la cible.

La cible reçoit les paquets RTP sur un port UDP choisi aléatoirement, et les obtiens a travers une socket comme d’habitude. Tel que défini dans RTP, chaque paquet a un marqueur de temps (timestamp) qui décrit l’heure de presentation de l’access unit (consultez la RFC3550 pour plus de details sur RTP). Étant donné qu’une access unit peut être plus volumineuse que ce que peut contenir le paquet RTP, elle peut être découpée en de multiples paquets RTP. La manière de le faire dépend du codec utilisé. Pour éviter de complexifier nous considèrerons que le receveur a un assembleur qui délivre chaque access unit ré-assemblée avec son marqueur temporel.

Dans les paragraphes suivants, nous nous intéresserons aux access units et a leur marqueurs de temps avant/apres qu’il soit passe par le transport reseau. Cela revient quasiment a étudier directement les paquets RTP et simplifie le raisonnement, c’est donc une hypothèse raisonnable.

Le problème : réseau et references de temps

Du cote émetteur, les access units sont produites de manière régulière. Pour une vidéo a 30 images par secondes, l’encodeur produit en général une access unit toutes les 33 millisecondes (ms). En réalité cela dépend du codec, mais nous ferons avec. L’illustration ci-dessous montre un flux d’access units émises en suivant une période de 33 ms (30 images par secondes).

Si le réseau était parfait, nous devrions recevoir exactement le même flux (avec le même intervalle de temps entre les access units), mais décalé d’un délai du à l’emission, la transmission, la réception et l’opération d’assemblage (voir l’illustration ci-dessous).

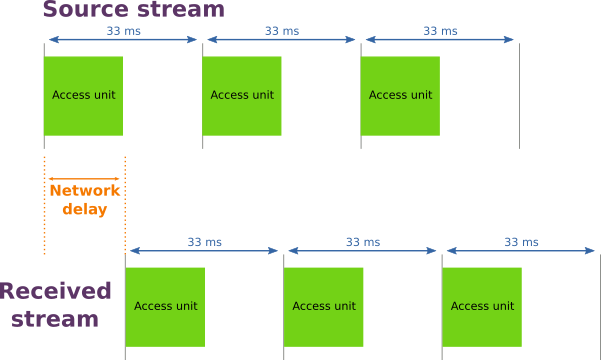
Mais dans le monde réel, le délai introduit par le réseau n’est pas constant. Il y a bien évidement un délai incompressible du au temps de propagation physique de l’information et au traitement des données, mais il y a aussi une part variable du à la congestion du réseau. Le véritable résultat a donc l’allure de l’illustration suivante.

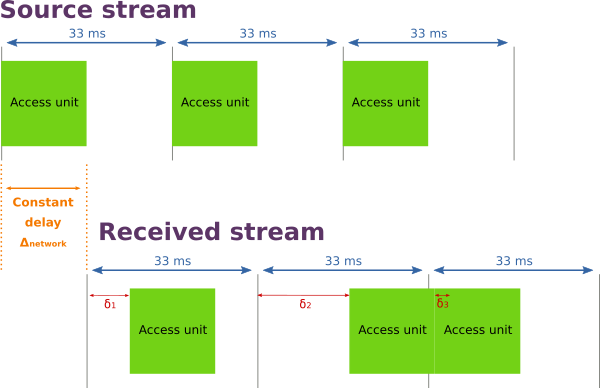
Chaque access unit est délivrée au receveur avec un délai relatif à son horloge de départ, qui varie en fonction des conditions du réseau. La latence d’une access unit peut être représentée comme suit :

\Delta_{frame}(n) = \Delta_{network} + \delta_n

Faisons un petit résume de la situation du receveur :

• il reçoit un flux d’access units avec leur marqueur de temps,
• les access units ne sont pas délivrées de manière régulière à cause de la congestion dans le réseau,
• les conditions du réseau évoluent au court du temps,
• la seule référence de temps disponible est le marqueur de temps disponible dans les paquets RTP.

Le défi est donc de trouver un moyen d’estimer la taille idéale de buffer (tampon) nécessaire pour jouer le contenu en minimisant l’impact des aléas du réseau tout en préservant l’interactivité.

Le « inter-arrival jitter » comme estimateur de l’état du réseau

Pour estimer la congestion du réseau, puis calculer une taille de tampon adéquate, nous avons besoin d’un indicateur. En cherchant des articles sur le sujet, j’ai trouvé le brouillon d’une RFC : Google Congestion Control Algorithm for Real-Time Communication. Cet algorithme déduit une « estimation du débit maximum du récepteur » (Receiver Estimated Maximum Bitrate ou REMB) en utilisant le inter-arrival jitter. Calculer un débit n’est pas exactement ce que nous cherchons mais il utilise uniquement les paquets RTP entrants et leur marqueurs de temps pour faire l’estimation. C’est déjà un bon point.

Inter-arrival jitter

Les marqueurs de temps des paquets reçus ne sont pas suffisants pour calculer la latence en valeur absolue de ce flux. Mais grâce à eux, nous avons une information de valeur : le délai théorique entre deux images qui se suivent. Il est équivalent au délai entre l’émission de deux images par l’émetteur. La différence entre ces deux marqueurs de temps T des images n et n-1 est nommé inter-departure time (délai inter-départs) et s’exprime de la manière suivante :

T(n) - T(n-1)

De l’autre coté, en tant que récepteur, nous pouvons enregistrer pour chaque image, son heure arrivée locale et calculer le délai t qui sépare deux images consécutives n et n-1. C’est ce que l’on appelle inter-arrival time (délai inter-arrivées) et s’exprime de la façon suivante :

t(n) - t(n-1)

Si l’on compare les délais inter-arrivée et inter-départ pour deux images consécutives, nous avons un indicateur de la congestion du réseau. Dans un réseau parfait il devrait être nul, en pratique il varie. On peut l’exprimer formellement comme suit :

J(n) = t(n) - t(n-1) - (T(n) - T(n-1))

Plus de détails sont disponible dans la RFC mentionnée précédemment.

Estimations

Observer le jitter est un bon indicateur de l’état du réseau car il représente la distance entre la situation idéale (le délai entre deux images au départ) et la réalité (le délai entre deux images à l’arrivée). Plus le jitter est éloigné de 0, plus le réseau est dérangé.

Le premier estimateur que l’on peut calculer est le jitter moyen. Il fourni une estimation du désordre au cours du temps, mais pour refléter correctement la réalité cette moyenne doit être glissante, avec une fenêtre de temps relativement courte. Dans l’implémentation de GCC dans Chromium, une moyenne glissante exponentielle est utilisée. Elle permet de conserver l’influence des échantillons mesurés récemment tout en lissant les fortes variations.

\alpha \text{ est le coefficient de la moyenne glissante} \\
J(n) \text{ est le inter-arrival jitter pour l'image } n \\
J_{avg}(n) \text{ est la moyenne glissante pour l'image } n \\
J_{avg}(n) = \alpha * J(n) + (1 - \alpha) * J_{avg}(n-1)

Le paramètre de lissage α doit être choisi en fonction du cas d’utilisation et de l’implémentation. Si l’on joue un flux à 30 images par seconde, une value de 0,1 pour α signifie que la moyenne s’applique sur 10 inter-arrival jitter, elle tient donc compte des 10 * 33ms = 330 dernières millisecondes.

La moyenne est un bon indicateur de départ, mais se révèle en fait relativement faible utilisé seul car elle est fortement sensible aux variations et ne fourni aucune véritable information sur la distribution du jitter. Pour être précis, on ne s’intéresse pas à la taille de buffer qui satisfait le jitter moyen, mais plutôt à celle qui permet de prendre en compte le jitter de la majorité des images. N’oublions pas que le but est d’avoir une expérience de lecture fluide de notre vidéo.

Nous cherchons donc un indicateur qui permette d’estimer une durée de buffer idéale afin de lisser l’impact du réseau pour la majorité des images. En disant cela on se rapproche de la solution : il nous faut un taille de buffer associée à un intervalle de confiance. En calculant l’écart type σ à partir des jitters mesurés, nous pouvons construite un intervalle autour du jitter moyen qui nous fournira la durée de buffer idéale pour 68% (la moyenne plus σ), 95% (la moyenne plus 2σ) voir même 99,7% (la moyenne plus 3σ) des images entrantes. Pour en savoir plus sur l’écart type et les intervalles de confiance, rendez-vous ici.

Nous pouvons donc calculer calculer une variance mobile sur les jitters en utilisant la moyenne exponentielle :

V(n) = \alpha * (J_{avg}(n) - J(n))^2 + (1 - \alpha) * V(n-1)

Puis en déduire l’écart type :

\sigma(n) = \sqrt{V(n)}

Prenons un exemple ! Après quelques secondes de streaming, le jitter moyen est de 15 ms et l’écart type de 37 ms. Si l’on considère un intervalle de confiance de 3σ, le calcul de la durée optimale du buffer est :

D_{buf}(n) = J_{avg}(n) + 3 * \sigma(n) = 15 + 3 * 37 = 126 \text{ ms}

En utilisant cette durée de buffer, nous savons couvrir 99,7% du jitter des images. Cette durée peut être ré-estimée régulièrement au cours du temps afin de toujours conserver le délai optimal. Ce faisant, la latence est conservée à sa valeur minimum tout en préservant une expérience de lecture fluide.

Conclusion

Calculer quelques indicateurs à partir du inter-arrival jitter est le procédé le plus simple que j’ai trouvé dans la littérature au cours de mes recherches sur le sujet. Il permet de fournir une expérience de lecture fluide tout en préservant une latence minimum. Il requiert, par ailleurs, peu d’information en entrée pour un indicateur fiable.

Remerciements

• Tristan Braud pour m’avoir aidé à comprendre les concepts derrière le jitter et les statistiques menant au calcul de taille de buffer.
• Rémi Peuvergne  pour ses conseils sur l’article et ses illustrations.

Références

• A Google Congestion Control Algorithm for Real-Time Communication [draft-ietf-rmcat-gcc-02]
  
• Chromium GCC implementation
• RFC3550 – RTP: A Transport Protocol for Real-Time Applications
• Wikipedia – Écart type
• Wikipedia – Intervalle de confiance