Some days ago, a friend showed me the following post The six common species of code, and I’ve been upset because it is easy to critize, or laugh at code writers, but it is harder to provide materials to write good algorithm. Obviously, they laugh, but as always … that’s all. A bit more seriously, reading this small Fibonacci example, I remembered old school times and I decided to create this article about Memoization.
Memoization is a way to write recusive algorithm in order to be faster. It uses a data cache to avoid multiple and redundant function calls. Indeed, sometimes, due to recursion, a data could be computed multiple times (this is typically the case with Fibonacci recursive implementation). The aim of memoization is to cache these data and reuse them when possible. In the following lines, we’ll look at an example applied on the Fibonacci serie.
Fibonacci serie standard implementation
The serie is defined by:
F(0) = 1 F(1) = 1 F(n) = F(n-1) + F(n-2)
It could be easily implemented by a recursive function like this:
unsigned int fibonacci(unsigned int n)
{
if (n == 0 || n == 1) {
return 1;
} else {
return fibonacci(n - 1) + fibonacci(n - 2);
}
}
But this naive form has a huge cost. Indeed, the number of call to fibonacci(…) will grow exponentially with n, thus the run time will explode. Run a fibonacci(100) could take hours and lead to a stack overflow. If we look carefully, we see that this implementation is quite inefficient. Each value of the serie is computed multiple times: F(n) will evaluate F(n-2) and F(n-1) which will evaluate F(n-2) again, etc.
A way to avoid this bad day effect is to use memoization.
Memoized implementation
The memoized implementation will use a small local data cache to store computed values. These values will be used instead of computing a series rank again. Here is a trivial C-styled implementation, assuming that the cache is allocated large enough to handle the call to fibonacci(n) and cache[0] = cache[1] = 1.
unsigned int *cache;
unsigned int fibonacci(unsigned int n)
{
unsigned int f;
if (cache[n] != 0)
f = cache[n];
else {
f = fibonacci(n - 2) + fibonacci(n - 1);
cache[n] = f;
}
return f;
}
Each time we ask for a fibonacci value, we look for it in the cache, and we compute it only if it is not available. Thus, as soon as a path of the call tree have been computed, all intermediate values are cached and a redundant call is almost costless.
This piece of code will have a linear run time function of n, but will still have exponential growth of the call stack. I’ll probably post a stack-size improved version of the algorithm in an update.
Performance evaluation
I compared the run times of the two implementations on my computer with a number of iterations between 10 and 55.
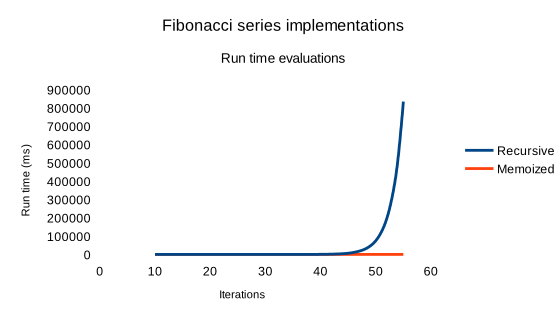
The memoized implementation is obviously faster, execution time begins to increase around 100,000 iterations (not represented here).
Conclusion
Memoization is a code optimization technique used to speed up algorithm by caching data to avoid redundants calculations. As we see with the Fibonacci series example, this method is really efficient.
But to be fair, we have to mention that a memoized solution is not perfect. Indeed, using a cache implies potentially big memory consumption. In our example, these kind of issues appears around 500,000 iterations. Plus, with such a high number we’ll have to deal with really big integer values and overflows.
As always, an optimisation method is not perfect, and should only be applied in a second time. In other words, a good software design is never base on optimizations: “Premature optimization is the root of all evil (or at least most of it) in programming.” (Donald Knuth).